Rebatimento de plano de rampa
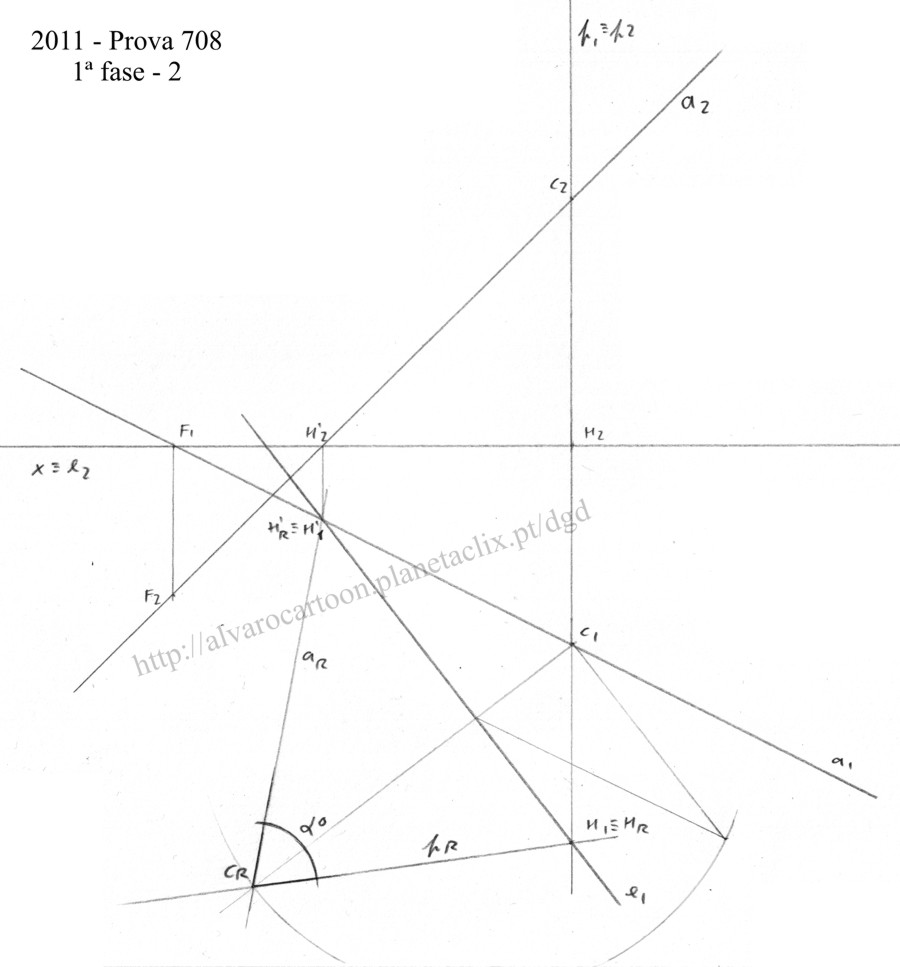
Por F1 desenhe uma perpendicular ao traço horizontal do plano, traço esse que será o eixo do rebatimento.
Abaixo, na perspectiva à direita temos o desenho do triângulo de rebatimento no espaço. Trata-se de um triângulo rectângulo, um triângulo em que um dos seus ângulos internos faz 90º. Um dos seus catetos é o segmento que vai de F1 ao eixo de rebatimento em projecção horizontal. O outro cateto (ao alto, na vertical) tem a medida da cota do ponto. A hipotenusa é a distância espacial, em V.G., do ponto F ao eixo de rebatimento.
É precisamente esse triângulo que tem de ser desenhado rigorosamente. O primeiro cateto já se encontra no desenho. O segundo para ser obtido, rebate-se o triângulo para o lado, ou seja, pega-se na medida da sua cota e coloca-se na perpendicular ao primeiro cateto sendo F1 o vértice comum aos dois catetos. E temos os dois catetos e a hipotenusa (no desenho a cinzento).
Com centro no ponto onde a perpendicular inicial e a hipotenusa cruzam ambos o eixo de rebatimentoabre-se o compasso até ao outro extremo da hipotenusa e roda-se essa medida para a perpendicular.
Onde o arco cruza a perpendicular temos o ponto rebatido. Neste caso, Fr.
Como F é um ponto do traço frontal do plano, ao ser rebatido passa por Fr. A distância do traço frontal do plano e do ponto F ao eixo de rebatimento é a mesma de Fr e do traço frontal rebatidos ao mesmo eixo. É nisto que consiste o rebatimento. Planificar um plano, rodando-o e colocando-o numa das projecções (horizontal ou frontal) em V.G (verdadeira grandeza).
E assim se rebate um plano de rampa.
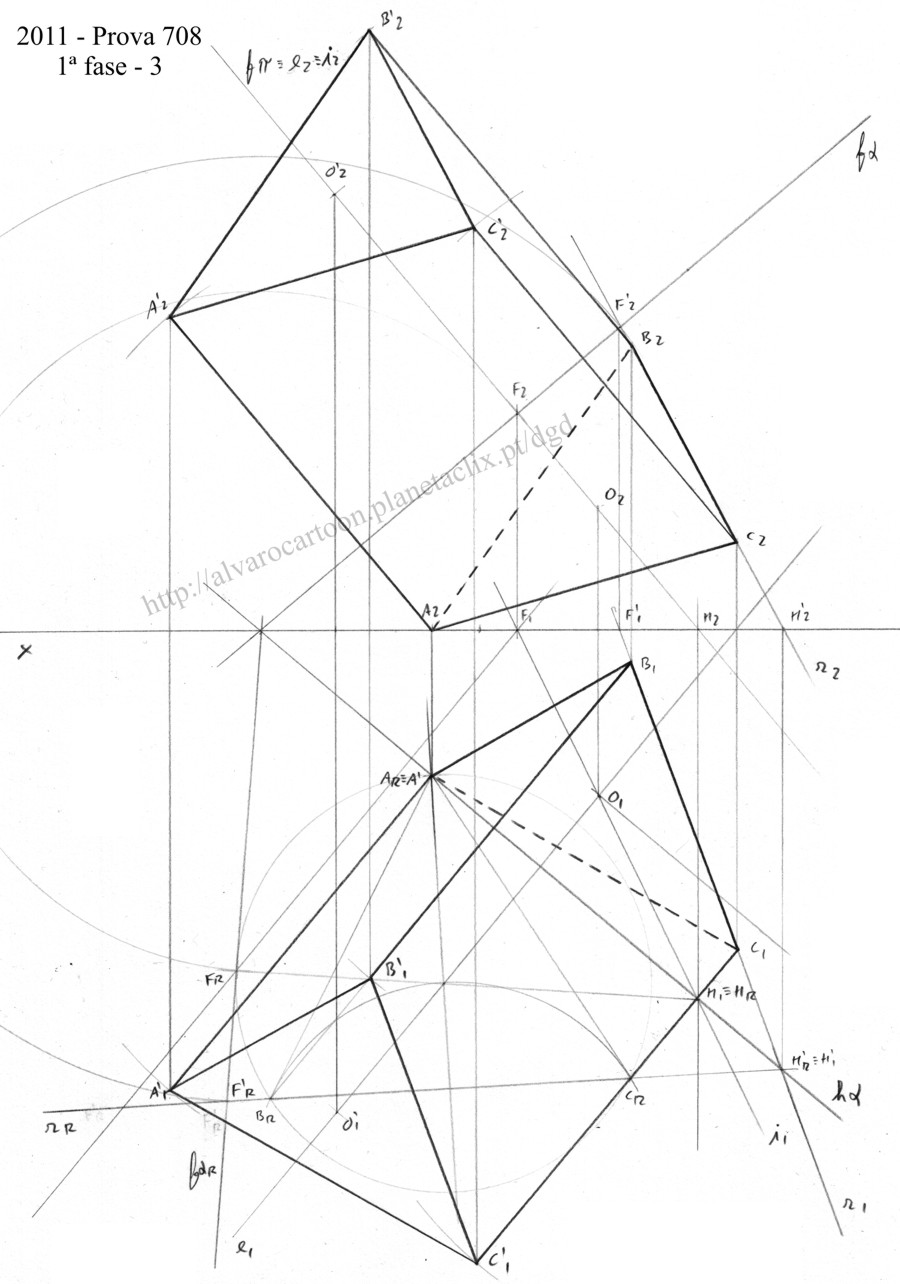
Para rebater outros pontos do plano passe rectas oblíquas que cruzem os dois traços dentro da folha de desenho. Para contra rebater rectas, pontos ou figuras planas segue-se o mesmo processo, inversamente.