Geometria Descritiva

domingo, 1 de junho de 2025

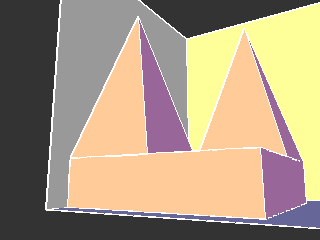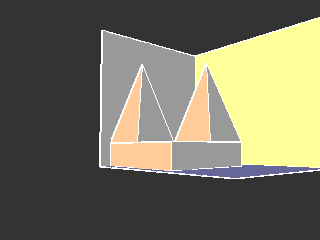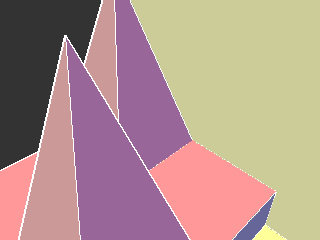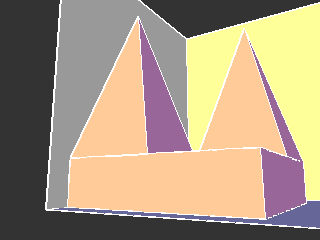
Sombra de uma pirâmide

Explicações de Geometria Descritiva por explicador experiente licenciado em Arquitectura em 1993. Do 10º, 11ª, 12º anos e faculdade.
Preparação para exame.
Localização: Parede, concelho de Cascais.
Nas aulas a particulares os valores encontram-se, pelo Art. 9º, isentos de IVA.
Contacto: explicador.gd@gmail.com

sábado, 10 de maio de 2025

Tabela de preços

Tabela de preços

Explicações de

Desenho - Geometria Descritiva - Autocad

para 10º, 11º, 12º anos e Faculdade - Preparação para os exames nacionais
por explicador experiente

Tabela de preços

Local: Parede
Nas aulas a particulares os valores encontram-se, pelo Art. 9º, isentos de IVA.

10º, 11º e 12º anos de escolaridade - 18 euros / hora

1 hora - 18 euros

1,5 horas - 27 euros

2 horas - 36 euros

Faculdade - 22 euros / hora

1 hora - 22 euros

1,5 horas - 33 euros

2 horas - 44 euros

Valor da deslocação
(a partir de 8 euros, consultar mapas abaixo para maior rigor)

Parede, Carcavelos, São Domingos de Rana, Oeiras e Estoril: + 8 euros de deslocação

Cascais (centro), Alcabideche, Manique, Porto Salvo e Paço de Arcos: + 10 euros de deslocação

Cascais (Torre, Birre, Areia), S. Marcos, Barcarena, Queijas, C. Quebrada: + 15 euros de deslocação

Cascais (Guincho), Queluz, Amadora, Algés, Lisboa: + 20 euros de deslocação

Clique nas imagens abaixo para as ampliar.

contacto: explicador.gd@gmail.com

Valores de deslocação

segunda-feira, 17 de junho de 2024

Exercícios de Geometria Descritiva quase impossíveis - Intersecção de rectas com sólidos

1 - X(4;8;4) e Y(0;4;9) são os pontos de intersecção da recta r com um cubo. A(0;10;2) é um dos vértices de uma das faces horizontais do sólido.
Determine as projecções da recta e do cubo.

2 - Determine o pontos X e Y de intersecção da recta r com um cilindro oblíquo situado no 1º diedro e de bases horizontais com 4 centímetros de raio. A(2;0;2) e A'(-2;4;6) são os extremos de uma geratriz do sólido. A recta r contém os pontos H(4;6;0) e J(-2;7;6).